Examining the results

After the results have been obtained, it is important to be able to examine the results easily. The results can be examined either numerically by inspecting numerical arrays or visually by plotting distributions of the nodes. In addition, the posterior distributions can be visualized during the learning algorithm and the results can saved into a file.

Plotting the results

The module plot offers some plotting basic functionality:

>>> import bayespy.plot as bpplt

The module contains matplotlib.pyplot module if the user needs that. For instance, interactive plotting can be enabled as:

>>> bpplt.pyplot.ion()

The plot module contains some functions but it is not a very comprehensive collection, thus the user may need to write some problem- or model-specific plotting functions. The current collection is:

• pdf(): show probability density function of a scalar

• contour(): show probability density function of two-element vector

• hinton(): show the Hinton diagram

• plot(): show value as a function

The probability density function of a scalar random variable can be plotted using the function pdf():

>>> bpplt.pyplot.figure()
<matplotlib.figure.Figure object at 0x...>
>>> bpplt.pdf(Q['tau'], np.linspace(60, 140, num=100))
[<matplotlib.lines.Line2D object at 0x...>]

(Source code, png, hires.png, pdf)

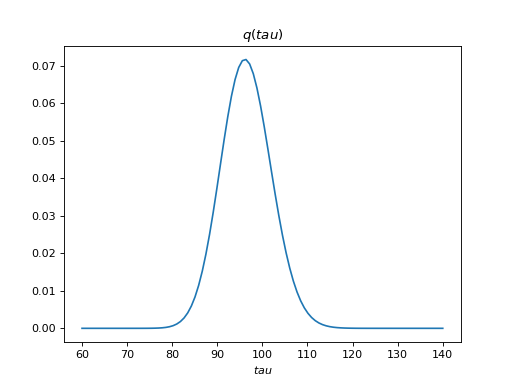
The variable tau models the inverse variance of the noise, for which the true value is . Thus, the posterior captures the true value quite accurately. Similarly, the function contour() can be used to plot the probability density function of a 2-dimensional variable, for instance:

>>> V = Gaussian([3, 5], [[4, 2], [2, 5]])
>>> bpplt.pyplot.figure()
<matplotlib.figure.Figure object at 0x...>
>>> bpplt.contour(V, np.linspace(1, 5, num=100), np.linspace(3, 7, num=100))
<matplotlib.contour.QuadContourSet object at 0x...>

(Source code, png, hires.png, pdf)

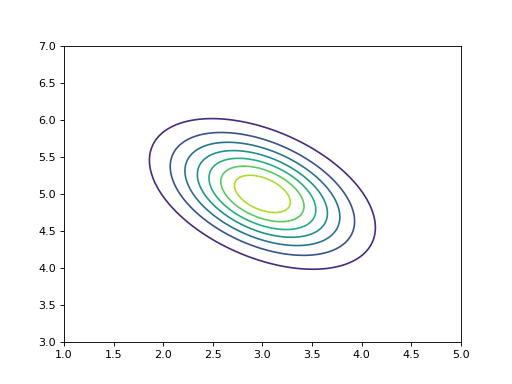
Both pdf() and contour() require that the user provides the grid on which the probability density function is computed. They also support several keyword arguments for modifying the output, similarly as plot and contour in matplotlib.pyplot. These functions can be used only for stochastic nodes. A few other plot types are also available as built-in functions. A Hinton diagram can be plotted as:

>>> bpplt.pyplot.figure()
<matplotlib.figure.Figure object at 0x...>
>>> bpplt.hinton(C)

(Source code, png, hires.png, pdf)

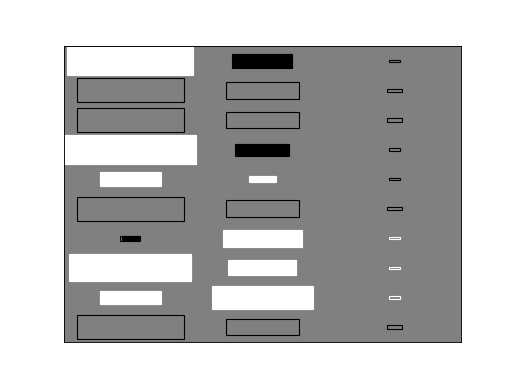
The diagram shows the elements of the matrix . The size of the filled rectangle corresponds to the absolute value of the element mean, and white and black correspond to positive and negative values, respectively. The non-filled rectangle shows standard deviation. From this diagram it is clear that the third column of has been pruned out and the rows that were missing in the data have zero mean and column-specific variance. The function hinton() is a simple wrapper for node-specific Hinton diagram plotters, such as gaussian_hinton() and dirichlet_hinton(). Thus, the keyword arguments depend on the node which is plotted.

Another plotting function is plot(), which just plots the values of the node over one axis as a function:

>>> bpplt.pyplot.figure()
<matplotlib.figure.Figure object at 0x...>
>>> bpplt.plot(X, axis=-2)

(Source code, png, hires.png, pdf)

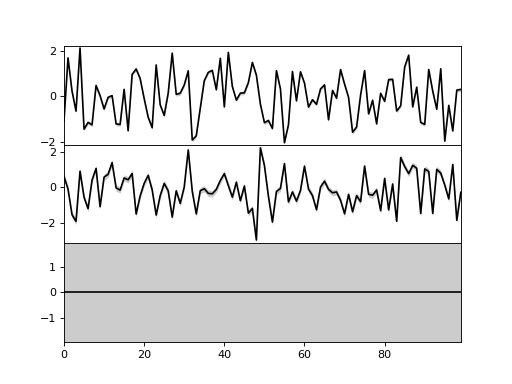
Now, the axis is the second last axis which corresponds to . As , there are three subplots. For Gaussian variables, the function shows the mean and two standard deviations. The plot shows that the third component has been pruned out, thus the method has been able to recover the true dimensionality of the latent space. It also has similar keyword arguments to plot function in matplotlib.pyplot. Again, plot() is a simple wrapper over node-specific plotting functions, thus it supports only some node classes.

Monitoring during the inference algorithm

It is possible to plot the distribution of the nodes during the learning algorithm. This is useful when the user is interested to see how the distributions evolve during learning and what is happening to the distributions. In order to utilize monitoring, the user must set plotters for the nodes that he or she wishes to monitor. This can be done either when creating the node or later at any time.

The plotters are set by creating a plotter object and providing this object to the node. The plotter is a wrapper of one of the plotting functions mentioned above: PDFPlotter, ContourPlotter, HintonPlotter or FunctionPlotter. Thus, our example model could use the following plotters:

>>> tau.set_plotter(bpplt.PDFPlotter(np.linspace(60, 140, num=100)))
>>> C.set_plotter(bpplt.HintonPlotter())
>>> X.set_plotter(bpplt.FunctionPlotter(axis=-2))

These could have been given at node creation as a keyword argument plotter:

>>> V = Gaussian([3, 5], [[4, 2], [2, 5]],
...              plotter=bpplt.ContourPlotter(np.linspace(1, 5, num=100),
...                                           np.linspace(3, 7, num=100)))

When the plotter is set, one can use the plot method of the node to perform plotting:

>>> V.plot()
<matplotlib.contour.QuadContourSet object at 0x...>

Nodes can also be plotted using the plot method of the inference engine:

>>> Q.plot('C')

This method remembers the figure in which a node has been plotted and uses that every time it plots the same node. In order to monitor the nodes during learning, it is possible to use the keyword argument plot:

>>> Q.update(repeat=5, plot=True, tol=np.nan)
Iteration 19: loglike=-1.221354e+02 (... seconds)
Iteration 20: loglike=-1.221354e+02 (... seconds)
Iteration 21: loglike=-1.221354e+02 (... seconds)
Iteration 22: loglike=-1.221354e+02 (... seconds)
Iteration 23: loglike=-1.221354e+02 (... seconds)

Each node which has a plotter set will be plotted after it is updated. Note that this may slow down the inference significantly if the plotting operation is time consuming.

Posterior parameters and moments

If the built-in plotting functions are not sufficient, it is possible to use matplotlib.pyplot for custom plotting. Each node has get_moments method which returns the moments and they can be used for plotting. Stochastic exponential family nodes have natural parameter vectors which can also be used. In addition to plotting, it is also possible to just print the moments or parameters in the console.

Saving and loading results

The results of the inference engine can be easily saved and loaded using VB.save() and VB.load() methods:

>>> import tempfile
>>> filename = tempfile.mkstemp(suffix='.hdf5')[1]
>>> Q.save(filename=filename)
>>> Q.load(filename=filename)

The results are stored in a HDF5 file. The user may set an autosave file in which the results are automatically saved regularly. Autosave filename can be set at creation time by autosave_filename keyword argument or later using VB.set_autosave() method. If autosave file has been set, the VB.save() and VB.load() methods use that file by default. In order for the saving to work, all stochastic nodes must have been given (unique) names.

However, note that these methods do not save nor load the node definitions. It means that the user must create the nodes and the inference engine and then use VB.load() to set the state of the nodes and the inference engine. If there are any differences in the model that was saved and the one which is tried to update using loading, then loading does not work. Thus, the user should keep the model construction unmodified in a Python file in order to be able to load the results later. Or if the user wishes to share the results, he or she must share the model construction Python file with the HDF5 results file.